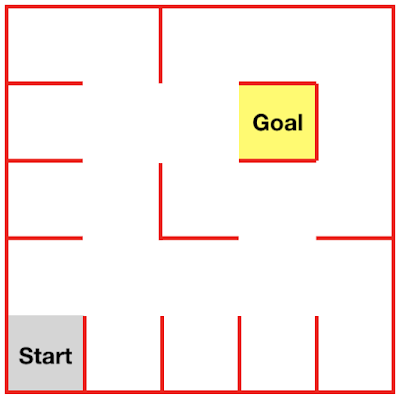
This is a maze that you won't reach the goal area if you follow the wall on your left or right hand side.
My experiences in designing micromouse and robotracer. 分享製作電腦鼠與自走車的經驗。
2018年12月12日 星期三
2018年11月27日 星期二
自走車線軌跡的曲率偵測 Curvature calculation in Robotrace contests
假設自走車的直線速度是 $v_C$ 而且被控制為定值,角速度是 $\omega_C$,重心位置與前方紅外線感測器用來估測線軌跡誤差控制中心點的距離為 $L$。
那麼控制中心點的速度 $v_{LC}$ 的大小,以及它與自走車直線速度方向的夾角為 $\phi$,可以用下列的方程式算出來
\[ v^2_{LC} = v^2_C + (\omega_C L)^2 \]
\[ \phi = \tan^{-1}\left(\dfrac{\omega_C L}{v_C}\right) \]
假設我們開始觀測的時間為 $t_0$,而且自走車的直線速度 $v_C$ 在 $t_0$ 到 $t$ 時間內的角度變化為 $\theta(t)-\theta(t_0)$。其中 \[ \theta(t) - \theta(t_0) = \int^t_{t_0} \omega_C(\tau) d\tau \]
那麼控制中心點速度 $v_{LC}$ 在 $t_0$ 到 $t$ 時間內的角度變化 $\alpha$ 就是 \[ \alpha = \theta(t)-\theta(t_0) + \tan^{-1}\left(\dfrac{\omega_C(t) L}{v_C}\right) - \tan^{-1}\left(\dfrac{\omega_C(t_0) L}{v_C}\right) \]
如果控制中心點能夠一直沿著線軌跡沒有誤差的移動,那麼在時間 $t$ 時線軌跡的曲率半徑 $r$ 就可以利用下列方程式來估測 \[ r = \dfrac{l}{\alpha} \] \[ l = \int^t_{t_0} v_{LC}(\tau) d\tau \]
另一個估測的方法是 \[ r = \dfrac{v_{LC}}{\dot{\alpha}} \] \[ \dot{\alpha} = \dfrac{d\alpha}{dt} = \omega_C + \dfrac{Lv_C}{v^2_C+(\omega_C L)^2} \dfrac{d\omega_C}{dt} \]
這是因為 \[ \dfrac{d\tan^{-1}(x)}{dx} = \dfrac{1}{1+x^2} \] 但是當控制中心點無法一直沿著線軌跡沒有誤差的移動時,該怎麼修正呢? 目前的想法是 \[ r_t = r - \delta x \] 其中 $r_t$ 是修正後的估測半徑,$\delta x$ 是控制中心點與線軌跡間的誤差大小。
假設我們開始觀測的時間為 $t_0$,而且自走車的直線速度 $v_C$ 在 $t_0$ 到 $t$ 時間內的角度變化為 $\theta(t)-\theta(t_0)$。其中 \[ \theta(t) - \theta(t_0) = \int^t_{t_0} \omega_C(\tau) d\tau \]
那麼控制中心點速度 $v_{LC}$ 在 $t_0$ 到 $t$ 時間內的角度變化 $\alpha$ 就是 \[ \alpha = \theta(t)-\theta(t_0) + \tan^{-1}\left(\dfrac{\omega_C(t) L}{v_C}\right) - \tan^{-1}\left(\dfrac{\omega_C(t_0) L}{v_C}\right) \]
如果控制中心點能夠一直沿著線軌跡沒有誤差的移動,那麼在時間 $t$ 時線軌跡的曲率半徑 $r$ 就可以利用下列方程式來估測 \[ r = \dfrac{l}{\alpha} \] \[ l = \int^t_{t_0} v_{LC}(\tau) d\tau \]
另一個估測的方法是 \[ r = \dfrac{v_{LC}}{\dot{\alpha}} \] \[ \dot{\alpha} = \dfrac{d\alpha}{dt} = \omega_C + \dfrac{Lv_C}{v^2_C+(\omega_C L)^2} \dfrac{d\omega_C}{dt} \]
這是因為 \[ \dfrac{d\tan^{-1}(x)}{dx} = \dfrac{1}{1+x^2} \] 但是當控制中心點無法一直沿著線軌跡沒有誤差的移動時,該怎麼修正呢? 目前的想法是 \[ r_t = r - \delta x \] 其中 $r_t$ 是修正後的估測半徑,$\delta x$ 是控制中心點與線軌跡間的誤差大小。
訂閱:
意見 (Atom)
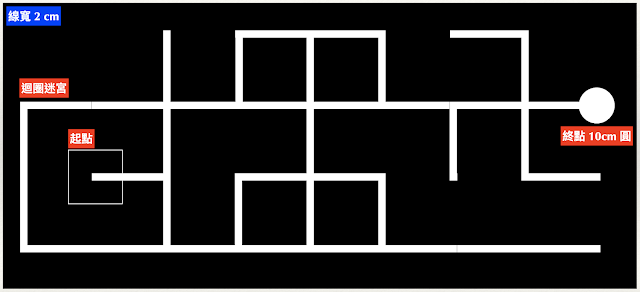
迴圈線迷宮(looped line maze)的搜尋與路徑簡化
迴圈線迷宮(如下圖),專指一個由直交線段組成的迷宮中,包含「迴圈」的路徑。在每年教育部主辦的「 電腦鼠暨智慧輪型機器人競賽 」中,屬於高中職與大專組的「 線迷宮鼠 」競賽活動。規則請參考以下連結 https://sites.google.com/gm.lhu.edu.tw/20...
-
這是一篇網路上可以參考的文章。 First Order Digital Filters - An Audio Cookbook 這一個數位濾波器的數學式是以下的樣子 (直流增益值為 1) \[ y_n = ay_{n-1} + (1-a)u_n \] 其中 $...
-
這是一個實際處理數位信號的例子,我覺得應該有助於整合上課學習到的概念。 左上角的藍色波形,是學生錄製的人聲 DO。 右上角是原始聲音的頻譜分析,以及 6 階 butterworth 低通濾波器的增益頻譜圖形。 左下角是將原始信號經過 6 階 butterwo...
-
這一篇是要配合鑑別出電腦鼠的系統特性時(直走或旋轉的動態),說明如何設計「速度回授控制器」的文章。 假設電腦鼠的系統特性如下,輸入是 PWM 數值,輸出是直線或角速度: \( G(s) = \frac{K_m}{\tau_ms+1} \) 其中 $s...