假設我們有以下三組資料 assume that we have the following 3 pairs of data,
$(x_1-\Delta, y_0)$, $(x_1, y_1)$, and $(x_1+\Delta, y_2)$
利用一個一元二次方程式來表示通過這三個點的曲線,參數為 $a, b, c$
A second order equation is used to represent a curve that passes these 3 points
$y_0 = a(x_1-\Delta)^2 + b(x_1-\Delta) + c$
$y_1 = ax_1^2 + bx_1 + c$
$y_2 = a(x_1+\Delta)^2 + b(x_1+\Delta) + c$
以下討論如何利用這三個點以及內差法,來找出當 $x=x_1+\alpha\Delta$ 的 y 值
The following discussion is used to predict what the $y$ value is, when $x=x_1+\alpha\Delta$
由於 Since
$y_0 = a(x_1-\Delta)^2 + b(x_1-\Delta) + c = y_1 - 2a\Delta x_1 + a\Delta^2 - b\Delta$
$y_2 = a(x_1+\Delta)^2 + b(x_1+\Delta) + c = y_1 + 2a\Delta x_1 + a\Delta^2 + b\Delta$
因此 Therefore
$y = a(x_1+\alpha\Delta)^2 + b(x_1+\alpha\Delta) + c = y_1 + \alpha(y_2-y_1) - \alpha(1-\alpha)a\Delta^2$
至於變數 $a$,可以利用以下關係求出來
and the variable $a$ can be found by using the following equation
$a = \frac{y_0+y_2-2y_1}{2\Delta^2}$
只是計算時,可以考慮使用 $a\Delta^2$,
It would be easier in calculation if we use the following equation
$a\Delta^2 = 0.5(y_0+y_2-2y_1)$
也就是說
$y = y_1 + \alpha(y_2-y_1) - 0.5\alpha(1-\alpha)(y_0+y_2-2y_1)$
其中的 $y_1 + \alpha(y_2-y_1)$,就是線性內差的結果,而 $- 0.5\alpha(1-\alpha)(y_0+y_2-2y_1)$ 可以看成是二次內差法針對一次內差法的修正項。
但也有可能我們必須求出當 $x=x_1-\Delta + \alpha\Delta$ 的 y 值,也就是自變數 $x$ 的值落在建表自變數的第一個與第二個之間的數值 It may be possible that we have to find the interpolation value that corresponds to $x=x_1-\Delta + \alpha\Delta$. This would occur when the $x$ value lies in the interval between the first and the second $x$ value of the table.
$y = a(x_1-\Delta+\alpha\Delta)^2 + b(x_1-\Delta+\alpha\Delta) + c = y_0 + (1-\alpha)(y_1-y_0) - \alpha(1-\alpha)a\Delta^2$
My experiences in designing micromouse and robotracer. 分享製作電腦鼠與自走車的經驗。
訂閱:
意見 (Atom)
迴圈線迷宮(looped line maze)的搜尋與路徑簡化
迴圈線迷宮(如下圖),專指一個由直交線段組成的迷宮中,包含「迴圈」的路徑。在每年教育部主辦的「 電腦鼠暨智慧輪型機器人競賽 」中,屬於高中職與大專組的「 線迷宮鼠 」競賽活動。規則請參考以下連結 https://sites.google.com/gm.lhu.edu.tw/20...
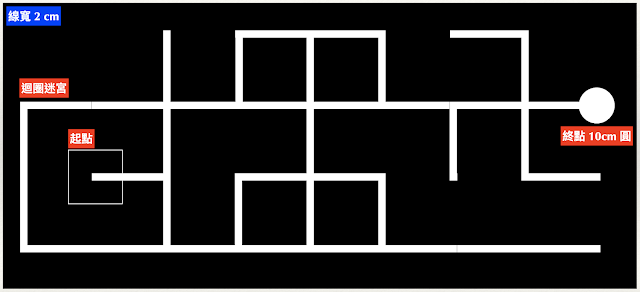
-
這是一篇網路上可以參考的文章。 First Order Digital Filters - An Audio Cookbook 這一個數位濾波器的數學式是以下的樣子 (直流增益值為 1) \[ y_n = ay_{n-1} + (1-a)u_n \] 其中 $...
-
這一篇是要配合鑑別出電腦鼠的系統特性時(直走或旋轉的動態),說明如何設計「速度回授控制器」的文章。 假設電腦鼠的系統特性如下,輸入是 PWM 數值,輸出是直線或角速度: \( G(s) = \frac{K_m}{\tau_ms+1} \) 其中 $s...
-
這是一個實際處理數位信號的例子,我覺得應該有助於整合上課學習到的概念。 左上角的藍色波形,是學生錄製的人聲 DO。 右上角是原始聲音的頻譜分析,以及 6 階 butterworth 低通濾波器的增益頻譜圖形。 左下角是將原始信號經過 6 階 butterwo...



