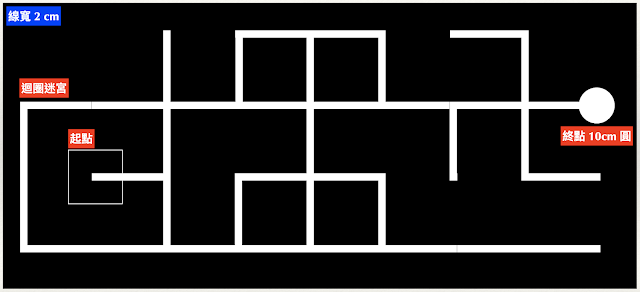
迴圈線迷宮(如下圖),專指一個由直交線段組成的迷宮中,包含「迴圈」的路徑。在每年教育部主辦的「電腦鼠暨智慧輪型機器人競賽」中,屬於高中職與大專組的「線迷宮鼠」競賽活動。規則請參考以下連結 https://sites.google.com/gm.lhu.edu.tw/2021tmirc/Home/Line-maze。
上圖的迴圈線迷宮,不管使用左手或是右手搜尋法則,都無法找到線迷宮的終點,更不用說是最短路徑了。若是輪型機器人上有編碼器,或是利用運動時間來計算行走距離時,就可以引用「電腦鼠走迷宮」的方法來找線迷宮的終點與最短路徑。
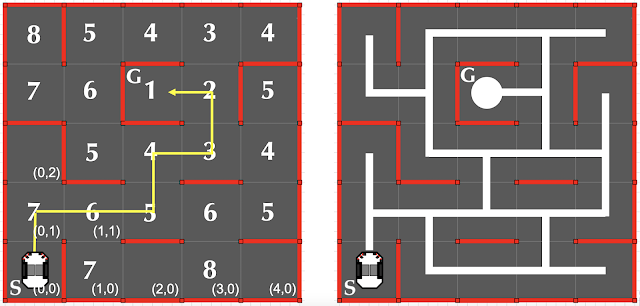
下圖是一個簡單的 5x5 電腦鼠迷宮的例子。右手邊是對應的線迷宮地圖,而左手邊是電腦鼠迷宮中習慣用的距離導向洪水演算法。當我們知道終點與起點的座標,以及路徑的組成時,洪水由終點出發,每經過一格,距離加 1,不管有沒有轉彎,直到洪水值出現在起點。此時,我們就可以從起點開始,藉由洪水數值,由大而小,反推回到終點,找到一條最短路徑。
接下來就剩下兩件事 1) 搜尋迷宮終點,以及 2) 建構地圖與路徑。線迷宮鼠(Line maze)與電腦鼠(Micromouse)走迷宮不同的是,線迷宮鼠的競賽並不知道終點座標的位置。因此,對於線迷宮鼠的迷宮,我們需要在走行的過程中,根據運動距離,1) 更新路口的座標(車頭為北方),以及 2) 確認路口的型態(參考下圖),並將這一些資料記錄在「地圖」資料中。當發現以左手或是右手法則搜尋終點時,當下的路口,所有的路徑都已經探索過時,就利用現有的地圖資料,找到鄰近尚未探索過的路徑後,再繼續以左手或是右手法則搜尋終點。這樣的做法,一直持續到抵達終點為止。
當我們以左手法則,在這一個簡單的迴圈迷宮搜尋終點,走到第 28 個路口時,發現這一個路口的路徑已經都探索過了,因此就可以利用儲存的地圖資料,右轉直走找到最近的第 5 個路口,還有一個標示為白色,尚未探索過的路徑。
回到這一條路徑後,繼續以左手法則探索,但到了第 23 個路口時,又發現這一個路口的路徑已經都探索過了,因此再利用儲存的地圖資料,直走左轉左轉,找到最近的第 18 個路口尚未探索過的路徑。接著在第 6 個路口時,又發現這一個路口的路徑已經都探索過了。再利用儲存的地圖資料,迴轉、直走、左轉,找到最近的第 17 個路口尚未探索過的路徑,當左轉後,就直接找到終點了。
沒有編碼器,也不計算距離...
但若是輪型機器人沒有編碼器,也無法計算距離時,有辦法避開這一些迴圈嗎?
還找不到一個好方法,待續...
部分解法
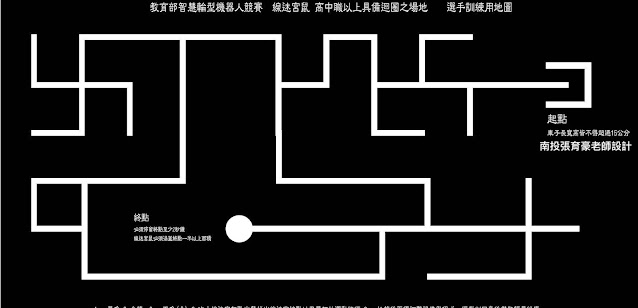
對於以下帶有迴圈的線迷宮(取自張育豪老師臉書照片),單用左手或是右手搜尋法則,都無法找到線迷宮的終點。如果我們加入以下的規則,
「當碰到連續的四次右轉(R)或是左轉(L) (即使中間穿插著直走(S)時),改變搜尋法則。」
以左手法則出發,就會有以下的結果。似乎有解,但還是無法對抗本文之前類似電腦鼠迷宮的例子,殘念...






沒有留言:
張貼留言