以下的方法,可以和 Kojima 先生的做法比較 The following method could be compared with the one proposed by Kojima san.
假設位置資料是 $x_1$,速度資料是 $x_2$,加速度資料是 $a$。那麼以狀態空間的方式來描述的話,就會是以下形式 Assume that $x_1$, $x_2$, and $a$ stand for position, velocity, and acceleration, respectively. The following state equation describes their relationship.
$\left[ \begin{matrix} \dot{x_1} \\ \dot{x_2} \end{matrix} \right]=\left[ \begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} \right]\left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right] + \left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] a$
如果位置資料的估測值是 $\hat{x}_1$,速度資料的估測值是 $\hat{x}_2$。那麼以下的狀態空間動態方程式,就可以用來估測位置資料,並且具備較高的解析度。這是利用 Luenberger observer 的概念來做的。Assume that $\hat{x}_1$, and $\hat{x}_2$, stand for position, and velocity estimations, respectively. The following dynamic equation derived from the idea of state observer could be used to estimate the position and velocity signals with better resolution and accuracy.
$\frac{d}{dt} \left[ \begin{matrix} \hat{x}_1 \\ \hat{x}_2 \end{matrix} \right]=\left[ \begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} \right]\left[ \begin{matrix} \hat{x}_1 \\ \hat{x}_2 \end{matrix} \right] + \left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] a + \left[ \begin{matrix} g_1 \\ g_2 \end{matrix} \right] (x_1 - \hat{x}_1)$
$g_1$ 與 $g_2$ 的設計可以用 $g_1=2\zeta \omega_n$,$g_2=\omega_n^2$,來設計,$\zeta$ 是 damping ratio ,$\omega_n$ 可以看成頻寬,$\zeta$ 可以選擇 [0.7, 1] 的範圍。Gains of $g_1$ and $g_2$ can be adjusted by using second order systems.
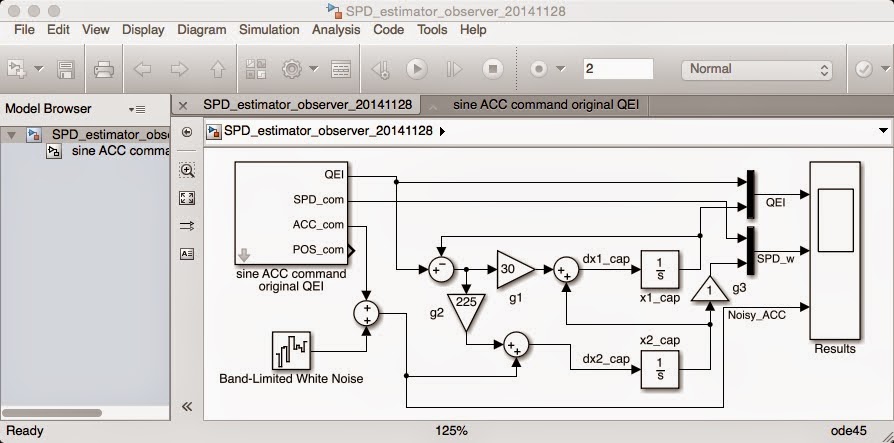
以下就是假設編碼器的解析度是 16 pulses/r 的模擬結果。其中加速度的資料來自加速規,而且我加了一些雜訊已接近真實情況。目前看起來還不錯。接下來就是數位化的工作。The following SIMULINK behavior model assumes that the resolution of a encoder is 16 pulses/r, and acceleration signal is added some white noise.
當我把編碼器輸出信號的單位弄錯時,下圖是錯誤的模擬結果,速度信號不對。The following incorrect results come from the wrong setting of the unit of position signals. The estimated velocity signal does not match the true one.
修正過後的結果,可以看出位置與速度都正確的跟上了。The followings are correct results.
放大來看,可以看出位置信號的解析度的確增加了,加速規雜訊的影響也不大。
整個估測器的 SIMULINK 行為模型。
產生模擬信號的SIMULINK 行為模型。
離散時間的模擬看起來也可以了,取樣時間設定為 $T_s$ = 1ms, Discrete time simulations with $T_s$ = 1ms seems OK now.