My experiences in designing micromouse and robotracer. 分享製作電腦鼠與自走車的經驗。
2017年12月24日 星期日
PD 控制的數位化設計
我們希望針對電腦鼠 PD 控制器的「數位化」做一些討論。
在 Peter 的文章 (Characterising the drive system on the micromouse) 中提到,電腦鼠的直走或旋轉運動,可以利用實驗資料找出對應的動態系統,還有對應的參數 $\tau_m$ 和 $K_m$
\[
G(s) = \frac{K_m}{\tau_ms + 1}
\]
這一篇文章要討論的是 PD 控制器,以及它數位化後的結果。Peter 也有一篇類似的文章 Designing the motor controller 。整體的系統架構是
\[
e(s) -> K_p+K_ds -> \frac{K_m}{\tau_ms + 1}
\]
其中 $e(s)$ 代表命令與位置輸出之間的誤差。
$G(s)$ 的狀態空間表示式是
\[
\dot{x}(t) = Ax(t) + Bu(t), \\
y(t) = Cx(t) \\
A = \begin{bmatrix}
0 & 1 \\
0 & \frac{1}{\tau_m}
\end{bmatrix}
, B = \begin{bmatrix}
0 \\
1
\end{bmatrix}
, C = \begin{bmatrix}
\frac{K_m}{\tau_m} & 0
\end{bmatrix}
\]
$G(s)$ 狀態空間表示式以取樣時間 $\Delta$ 數位化後的結果 $G(z)$ 是
\[
x[n+1] = Fx[n] + Gu[n], \\
y[n] = Hx[n] \\
F = e^{A\Delta}, B =
, C = \begin{bmatrix}
\frac{K_m}{\tau_m} & 0
\end{bmatrix}
\]
2017年10月1日 星期日
加速規信號的零點校正
這一個問題緣起於我們希望對四旋翼直升機上的加速度信號做「零點校正」。
假設從 MPU6500 取得的加速度信號分別是 $x_i$, $y_i$, 以及 $z_i$,這三個軸未知零點的數值分別是 $x_0$, $y_0$, 以及 $z_0$,而且重力加速度 $g$ 不變。
如果我們量測三次,得到 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$ 三組數據,那麼我們就可以有以下三個關係式
\[ (x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2 = g^2, \] \[ (x_2-x_0)^2+(y_2-y_0)^2+(z_2-z_0)^2 = g^2, \] \[ (x_3-x_0)^2+(y_3-y_0)^2+(z_3-z_0)^2 = g^2. \]
只是從 MPU6500 取得的加速度信號通常很髒,因此 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$ 這三組數據,究竟應該是濾波後的結果,還是不需要呢?另外,反矩陣的計算其實對寫程式而言不是很友善,因此如何利用其他的演算法(如 Recursive Least Square的方法)來實現,也是值得討論。
假設從 MPU6500 取得的加速度信號分別是 $x_i$, $y_i$, 以及 $z_i$,這三個軸未知零點的數值分別是 $x_0$, $y_0$, 以及 $z_0$,而且重力加速度 $g$ 不變。
如果我們量測三次,得到 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$ 三組數據,那麼我們就可以有以下三個關係式
\[ (x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2 = g^2, \] \[ (x_2-x_0)^2+(y_2-y_0)^2+(z_2-z_0)^2 = g^2, \] \[ (x_3-x_0)^2+(y_3-y_0)^2+(z_3-z_0)^2 = g^2. \]
第一式減去第二式可以得到
\[ x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 = 2(x_1-x_2)x_0 + 2(y_1-y_2)y_0 + 2(z_1-z_2)z_0 \]
第一式減去第三式可以得到
\[ x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 = 2(x_1-x_3)x_0 + 2(y_1-y_3)y_0 + 2(z_1-z_3)z_0 \]
\[ x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 = 2(x_1-x_2)x_0 + 2(y_1-y_2)y_0 + 2(z_1-z_2)z_0 \]
第一式減去第三式可以得到
\[ x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 = 2(x_1-x_3)x_0 + 2(y_1-y_3)y_0 + 2(z_1-z_3)z_0 \]
第二式減去第三式可以得到
\[ x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2 = 2(x_2-x_3)x_0 + 2(y_2-y_3)y_0 + 2(z_2-z_3)z_0 \]
寫成矩陣的形式
\[
\left[
\begin{array}
.2(x_1-x_2) & 2(x_1-x_3) & 2(x_2-x_3) \\
2(y_1-y_2) & 2(y_1-y_3) & 2(y_2-y_3) \\
2(z_1-z_2) & 2(z_1-z_3) & 2(z_2-z_3)
\end{array}
\right]
\left[
\begin{array}
.x_0 \\
y_0 \\
z_0
\end{array}
\right] =
\left[
\begin{array}
.x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 \\
x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 \\
x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2
\end{array}
\right]
\]
\[ x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2 = 2(x_2-x_3)x_0 + 2(y_2-y_3)y_0 + 2(z_2-z_3)z_0 \]
寫成矩陣的形式
\[
\left[
\begin{array}
.2(x_1-x_2) & 2(x_1-x_3) & 2(x_2-x_3) \\
2(y_1-y_2) & 2(y_1-y_3) & 2(y_2-y_3) \\
2(z_1-z_2) & 2(z_1-z_3) & 2(z_2-z_3)
\end{array}
\right]
\left[
\begin{array}
.x_0 \\
y_0 \\
z_0
\end{array}
\right] =
\left[
\begin{array}
.x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 \\
x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 \\
x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2
\end{array}
\right]
\]
因此,這三個軸未知零點的數值 $x_0$, $y_0$, 以及 $z_0$,就可以利用以下的公式求出來,當然前提是反矩陣存在。
\[
\left[
\begin{array}
.x_0 \\
y_0 \\
z_0
\end{array}
\right] =
\left[
\begin{array}
.2(x_1-x_2) & 2(x_1-x_3) & 2(x_2-x_3) \\
2(y_1-y_2) & 2(y_1-y_3) & 2(y_2-y_3) \\
2(z_1-z_2) & 2(z_1-z_3) & 2(z_2-z_3)
\end{array}
\right]^{-1}
\left[
\begin{array}
.x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 \\
x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 \\
x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2
\end{array}
\right]
\]
\[
\left[
\begin{array}
.x_0 \\
y_0 \\
z_0
\end{array}
\right] =
\left[
\begin{array}
.2(x_1-x_2) & 2(x_1-x_3) & 2(x_2-x_3) \\
2(y_1-y_2) & 2(y_1-y_3) & 2(y_2-y_3) \\
2(z_1-z_2) & 2(z_1-z_3) & 2(z_2-z_3)
\end{array}
\right]^{-1}
\left[
\begin{array}
.x_1^2 + y_1^2 + z_1^2 - x_2^2 - y_2^2 - z_2^2 \\
x_1^2 + y_1^2 + z_1^2 - x_3^2 - y_3^2 - z_3^2 \\
x_2^2 + y_2^2 + z_2^2 - x_3^2 - y_3^2 - z_3^2
\end{array}
\right]
\]
只是從 MPU6500 取得的加速度信號通常很髒,因此 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$ 這三組數據,究竟應該是濾波後的結果,還是不需要呢?另外,反矩陣的計算其實對寫程式而言不是很友善,因此如何利用其他的演算法(如 Recursive Least Square的方法)來實現,也是值得討論。
2017年4月24日 星期一
2017年4月21日 星期五
一階的數位 IIR 低通濾波器
這是一篇網路上可以參考的文章。
First Order Digital Filters - An Audio Cookbook
這一個數位濾波器的數學式是以下的樣子 (直流增益值為 1)
\[ y_n = ay_{n-1} + (1-a)u_n \]
其中 $y_n$、$y_{n-1}$ 與 $u_n$ 分別代表濾波器現在的輸出值、濾波器過去一個取樣時間的輸出值,和現在的原始信號。
$a$ 這一個係數定義成 \[ a = e^{-\pi f/F_n} \]
其中 $F_n$ 是取樣頻率 $F_s$ 的一半,$f$ 代表設定的頻寬。
畫出對應的頻率響應圖,的確一如預期。
MATLAB 程式
First Order Digital Filters - An Audio Cookbook
$a$ 這一個係數定義成 \[ a = e^{-\pi f/F_n} \]
其中 $F_n$ 是取樣頻率 $F_s$ 的一半,$f$ 代表設定的頻寬。
畫出對應的頻率響應圖,的確一如預期。
Matlab 的程式碼
% constants
Fs=20000; % sampling rate
t=1/Fs; % sampling interval
Fn=Fs/2; % Nyquist frequency
numPts=2^13; % number of points of analysis
%
n = [0.002 0.01 0.05 0.1 0.2];
a = exp(-pi*n*Fn/Fn);
%
% First order IIR filter
% y(n) = a*y(n-1) + (1-a)*u(n)
% find frequency response
%
h1 = figure(1);
set(h1,'color','white');
for i = 1:5
[h,w] = freqz([1-a(i) 0],[1 -a(i)], numPts);
% calculate dB values, for power quantities
y(:,i) = 20*log10(abs(h));
end;
semilogx(w*10000/pi, y,'-.','LineWidth',2);
ax3 = gca;
set(ax3,'fontsize',14,'linewidth',1.0);
grid;
xlabel('frequency in Hz','fontsize',16);
ylabel('Gain in dB, 20log_{10}(Gain)','fontsize',16);
title('Frequency Responses, y_n = ay_{n-1} + (1-a)u_n, a=exp(-\pif/F_n), F_n=10000Hz','fontsize',16);
axis([2 10^4 -45 5])
l1=legend('f = 20Hz','f = 100','f = 500','f = 1000','f = 2000','Location','SouthWest')
set(l1,'fontsize',16);
但為何如此呢?
我知道了!其實上述的想法,並非是一個公式,而是近似如此(工程師觀點)!
為了證明這樣的觀點,我自己針對特定的頻率值 $\pi f/F_n$ 把頻率響應在認為是3dB頻寬與實際值做了一下比較
\[ \frac{Y(z)}{U(z)} = \frac{1-e^{-\pi f/F_n}}{z-e^{-\pi f/F_n}} \]
其中 $z = e^{-j\Omega}$ ,而且 $\Omega = e^{-j\pi f/F_n}$。
結果如下:
MATLAB 程式
h2 = figure(2);
set(h2,'color','white');
aa = (0.02:0.02:0.4)*pi;
bb= 1-exp(-aa);
cc=exp(j*aa)-exp(-aa);
dd = abs(bb)./abs(cc);
plot(aa,dd,'--o','LineWidth',2);grid;
ax2 = gca;
set(ax2,'fontsize',14,'linewidth',1.0);
axis([0.02*pi 0.4*pi 0.4 0.8]);
xlabel('Values of \pif/F_n','fontsize',16);
title('Ratio of abs(1-exp(\pif/F_n))/abs(exp(-j\pif/F_n))-exp(-\pif/F_n))','fontsize',16);
當 $f/F_n$ 在 0.4 以下,也就是 $\pi f/F_n$ 在 1.26 以下時,這一個數位低通濾波器關於增益的頻率響應,在 $\pi f/F_n$ 的位置上的確是在 3dB (0.707) 左右的位置。
由上圖可以看出,這樣的想法,在 $\pi f/F_n$ 越來越大時,會越不準!只是因為是低通濾波器的關係,以工程師的觀點來看,應該還是可以接受的!
由上圖可以看出,這樣的想法,在 $\pi f/F_n$ 越來越大時,會越不準!只是因為是低通濾波器的關係,以工程師的觀點來看,應該還是可以接受的!
但究竟是如何看出這樣的關係呢?
想的出來的話,鐵定功力大增!
很吃力的一篇技術文章!
2017年4月10日 星期一
數位信號處理教學心得 part I - IIR低通濾波器設計
這是一個實際處理數位信號的例子,我覺得應該有助於整合上課學習到的概念。
左上角的藍色波形,是學生錄製的人聲 DO。
右上角是原始聲音的頻譜分析,以及 6 階 butterworth 低通濾波器的增益頻譜圖形。
左下角是將原始信號經過 6 階 butterworth 低通濾波器後的波形,振幅有些縮小了。
右下角是濾波過後信號的頻譜分析,配合右上角的的圖形,希望學生可以很容易理解低通濾波器針對信號頻譜的相乘作用。(因為對現性非時變系統而言,輸出信號是由輸入信號與系統的脈衝響應做摺積而得,也可以看成是輸入信號的頻譜與系統轉移函數的頻譜相乘)
以下是 MATLAB 的原始程式碼,其中也包含如何在微控制器中去實現對應的低通濾波器,只是程式中並沒有考慮整數運算的限制,全都是浮點數運算。
clear;
clc;
%
Fs = 44100;
y1 = audioread('d974323027.wav');
u = y1(1:44101,1);
n1=1:max(size(u));
tt=n1/Fs;
yy = [tt' u];
[b,a]=butter(6,0.03);
sys = tf(b, a, 1/Fs);
bs = max(size(b));
sb=zeros(size(u));
for k = bs:max(size(u))
sbk = sb(k-1:-1:k-6);
uk = u(k:-1:k-6);
sb(k) = -a(2:7)*sbk+b*uk;
end
sz = max(size(sb));
u2 = u(15001:25000);
sb2= sb(15001:25000);
fu = fft(u2);
fb = fft(sb2);
df = 0:Fs/max(size(u2)):(max(size(u2))-1)*Fs/max(size(u2));
dfb= 0:Fs/max(size(sb2)):(max(size(sb2))-1)*Fs/max(size(sb2));
[mag, phase]=bode(sys, df*2*pi);
mag2 = squeeze(mag);
h = figure(1);
set(h,'color','white');
n2=1:max(size(sb));
subplot(221);plot(n1,u,'r');axis([4000 14000 -0.8 0.8]);
ax1 = gca;
set(ax1,'fontsize',14,'linewidth',1.0);
title('Original sound signal','fontsize',16);
xlabel('points','fontsize',16);
%
subplot(223);plot(sb,'b');axis([4000 14000 -0.8 0.8]);
ax3 = gca;
set(ax3,'fontsize',14,'linewidth',1.0);
title('Filtered sound signal','fontsize',16);
xlabel('points','fontsize',16);
%
subplot(222);
[ax,h1,h2]=plotyy(df(1:400),abs(fu(1:400)),df(1:400),mag2(1:400));
grid;
axis(ax(1),[0 1500 0 1200]);
axis(ax(2),[0 1500 0 1.2]);
set(ax(1),'fontsize',14,'linewidth',1.0);
h1.Color = 'blue';
h1.LineWidth = 1;
h2.LineWidth = 1;
set(ax(2),'fontsize',14,'linewidth',1.0);
title('Spectrum of the original sound signal and filter','fontsize',16);
xlabel('Hz','fontsize',16);
ylabel(ax(2),'Gain','fontsize',16);
%
subplot(224);
p4 = plot(dfb,abs(fb),'b');
axis([0 1500 0 1200]);
set(p4,'linewidth',1);
ax4 = gca;
set(ax4,'fontsize',14,'linewidth',1.0);
grid;
title('Spectrum of the filtered sound signal','fontsize',16);
xlabel('Hz','fontsize',16);
訂閱:
意見 (Atom)
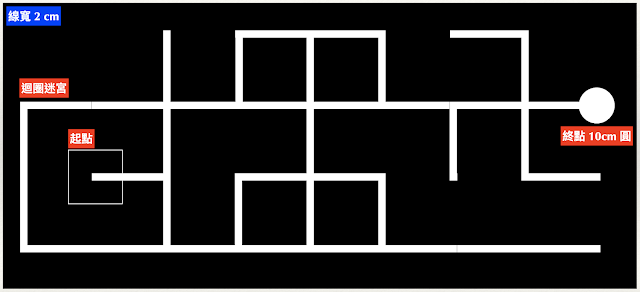
迴圈線迷宮(looped line maze)的搜尋與路徑簡化
迴圈線迷宮(如下圖),專指一個由直交線段組成的迷宮中,包含「迴圈」的路徑。在每年教育部主辦的「 電腦鼠暨智慧輪型機器人競賽 」中,屬於高中職與大專組的「 線迷宮鼠 」競賽活動。規則請參考以下連結 https://sites.google.com/gm.lhu.edu.tw/20...
-
這是一篇網路上可以參考的文章。 First Order Digital Filters - An Audio Cookbook 這一個數位濾波器的數學式是以下的樣子 (直流增益值為 1) \[ y_n = ay_{n-1} + (1-a)u_n \] 其中 $...
-
這是一個實際處理數位信號的例子,我覺得應該有助於整合上課學習到的概念。 左上角的藍色波形,是學生錄製的人聲 DO。 右上角是原始聲音的頻譜分析,以及 6 階 butterworth 低通濾波器的增益頻譜圖形。 左下角是將原始信號經過 6 階 butterwo...
-
這一篇是要配合鑑別出電腦鼠的系統特性時(直走或旋轉的動態),說明如何設計「速度回授控制器」的文章。 假設電腦鼠的系統特性如下,輸入是 PWM 數值,輸出是直線或角速度: \( G(s) = \frac{K_m}{\tau_ms+1} \) 其中 $s...



















